Fradrag utarbeide papirarbeid for systemet. Redusert system for fradrag
Vanligvis som et komplett system av rester modulo m ta de minste ikke-negative restene
0,1,...,m − 1eller absolutt minste rester som består av tall
,ved oddetall m og tall
i tilfelle jevn m .
se også
Litteratur
- I. M. Vinogradov Grunnleggende om tallteori. - M.-L.: Stat. utg. teknisk og teoretisk litteratur, 1952. - 180 s.
Wikimedia Foundation. 2010 .
Se hva "Full Deduction System" er i andre ordbøker:
Modulo m, ethvert sett med heltall som inneholder ett tall fra hver klasse med tall modulo m (to heltall a og b tilhører samme klasse modulo m hvis a b er delelig med m; se Rest). Som P. med. i. oftere… …
Modulo m er ethvert sett med heltall som er uforlignelige modulo en. Vanligvis som P. med. i. modulo de minste ikke-negative restene 0, 1, . . ., m 1 eller de absolutt minste rester som består av tallene 0, +1, . . ., i … … Matematisk leksikon
Del av et komplett system med fradrag (se Komplett system rester) som består av coprimtall med modul m. P. s. i. inneholder φ(m) tall [φ(m) er antall tall relativt primtall til m og mindre enn m]. Eventuelle φ(m)-tall som ikke er sammenlignbare modulo m og ... ... Stor sovjetisk leksikon
Sammenligning modulo et naturlig tall n i tallteori er en ekvivalensrelasjon på ringen av heltall relatert til delbarhet med n. En kvotientring med hensyn til denne relasjonen kalles en restring. Settet med tilsvarende identiteter og ... ... Wikipedia
I tallteori er kongruens modulo et naturlig tall n en ekvivalensrelasjon på settet med heltall gitt av det utpekte tallet, relatert til delbarhet med det. Kvotientrommet i denne relasjonen kalles "ringen ... ... Wikipedia
Symmetrien til et snøfnugg er assosiert med en gruppe rotasjoner med en vinkel som er et multiplum av 60°. En endelig gruppe er en algebraisk gruppe som inneholder et begrenset antall elementer (dette tallet kalles rekkefølgen). Videre antas gruppen å være multiplikativ, det vil si operasjonen i ... ... Wikipedia
Funksjonen til kanten kan representeres av en potensserie. Ekskluder, viktigheten av klasse A. f. er definert som følger. For det første er denne klassen ganske bred: den dekker de fleste funksjonene man møter i de grunnleggende spørsmålene i matematikk og dens ... ... Matematisk leksikon
I Innhold: I. Grunnskoleopplæring generelt. II. Grunnskoleutdanning i utlandet: Østerrike-Ungarn, England, Belgia, Bulgaria, Tyskland, Holland, Danmark, Spania, Italia, Norge, Portugal, Romania, Serbia, ... ... Encyclopedic Dictionary F.A. Brockhaus og I.A. Efron
- - ble født 26. mai 1799 i Moskva, på Nemetskaya Street i huset til Skvortsov; døde 29. januar 1837 i St. Petersburg. På sin fars side tilhørte Pushkin en gammel adelig familie, stammet, ifølge slekten, fra en innfødt "fra ... ... Stort biografisk leksikon
Settet med lukkede formler for predikatlogikk for det første trinnet. E. t. Th(K) av klassen K av algebraiske signatursystemer kalt. settet med alle lukkede formler for logikken til predikatene i det første trinnet i signaturen sann på alle systemer fra klassen K. Hvis klassen ... ... Matematisk leksikon
I henhold til egenskapen til sammenligninger nr. 15, tall av samme klasse modulo m har med modul m samme NOD. Klassene der det er lik 1 er spesielt viktige.
Tar vi ett tall fra hver av disse klassene, får vi redusert fradragssystem modulo m. Vanligvis er det isolert fra systemet med minst ikke-negative rester modulo m.
Redusert system av minst ikke-negative rester modulo m betegnet U m.
Antall tall i det reduserte systemet av rester modulo m, er åpenbart lik φ( m).
Eksempel:
Det reduserte systemet av rester modulo 15 er (1; 2; 4; 7; 8; 11; 13; 14). Legg merke til at φ(15)=(5–1)∙(3–1)= 8 og faktisk er det nøyaktig 8 elementer i det reduserte systemet av rester modulo 15.
Uttalelse 1
Enhver φ( m) tall parvis uforlignelig modulo m og coprime med m, danner et redusert system av rester.
(Bevis er åpenbart som i påstand 1 punkt 2)
Uttalelse 2
Hvis ( en, m) = 1, x går gjennom det reduserte systemet av rester modulo m, deretter øks går også gjennom det reduserte systemet av rester modulo m. (Beviset er åpenbart som i påstand 2 punkt 2).
Omvendt element.
Elementet sies å b kalt omvendt til en modulo m, hvis a∙b≡1(mod m) og skrive b ≡ en–1 (mod m).
Generelt sett trenger ikke klassisk tallteori et slikt begrep som et omvendt element, som kan sees ved å lese for eksempel med. Imidlertid bruker kryptologi restsystemer både i tallteoretiske og algebraiske aspekter, og derfor introduserer vi konseptet om et inverst element for å gjøre det enklere å presentere kryptologiens algebraiske grunnlag.
Spørsmålet oppstår om for alle elementer modulo m det er en invers (ved multiplikasjon), og hvis for noen elementer den inverse eksisterer, hvordan finne den?
For å svare på dette spørsmålet bruker vi den utvidede Euclid-algoritmen. Tenk først på coprimtallene en og modul m. Da, åpenbart, en,m)=1. Den utvidede Euclid-algoritmen lar deg få tall x Og y, slik at øks+my=(en,m), eller, som er det samme, øks+min=1. Fra det siste uttrykket får vi sammenligningen øks+min≡1(mod m). For så vidt min≡0(mod m), deretter øks≡1(mod m), som betyr at antallet oppnådd ved hjelp av den utvidede euklidiske algoritmen x bare er det ønskede inverse elementet til tallet en modulo m.
Eksempel.
en=5, m=7. Ønsket å finne en-1 mod m.
La oss bruke den utvidede Euklids algoritme.
Omvendt trekk:
1=5–2∙2=5–(7–5∙1)∙2=5∙3–7∙2.
x=3, y=–2.
5 -1 ≡3 (mod 7)
Sjekk: 5∙3=15. 15≡1 (mod 7).
Faktisk er 3 det inverse av 5 modulo 7.
Så, på en konstruktiv måte, var vi overbevist om at for tall coprime med en modul, er det en invers modulo dette. Og er det inverse elementer for tall som ikke er coprime med modulen?
La være ( en,m)=d≠1. Da kan a og m representeres som en=d∙en 1 , m=d∙m en . Anta at for a er det et inverst element modulo m, det vil si, b: en∙b≡1(mod m). Deretter en∙b=m∙k+1. Eller, hva er det samme, d∙en 1 ∙b= d∙m 1 ∙k+1. Men så, ved setning 2 fra §1 punkt 1, på grunn av det faktum at både venstre side av denne ligningen og første ledd på høyre side er delelig med d, deretter d\1, som ikke er sant fordi d≠1. Vi har kommet til en selvmotsigelse, derfor er antagelsen om eksistensen av et inverst element feil.
Så vi bare beviste
reversibilitetsteorem
en-1 (mod m) (en, m) = 1.
Når vi oppsummerer alle argumentene i dette avsnittet, kan vi si at bare coprimtall med modul er reversible, og du kan finne deres resiproke ved å bruke den utvidede Euklids algoritme.
eller påfølgende s tall.
Dette systemet kalles et komplett system av tall som ikke er sammenlignbare i modul s eller komplett system av rester modulo s. Det er åpenbart at evt s fortløpende tall danner et slikt system.
Alle tall som tilhører samme klasse har mange felles egenskaper, derfor kan de i forhold til modulen betraktes som ett tall. Hvert tall som inngår i sammenligningen som en summand eller faktor kan erstattes, uten å krenke sammenligningen, med et tall som kan sammenlignes med det, dvs. med et nummer som tilhører samme klasse.
Det andre elementet som er felles for alle tallene i en gitt klasse er den største felles deleren for hvert element i denne klassen og modulen s.
La være en Og b sammenlignbare modulo s, deretter
Teorem 1. Hvis i øks+b i stedet for x la oss ordne alt s medlemmer av det komplette tallsystemet
Derfor alle tall øks+b, hvor x=1,2,...s-1 er ikke sammenlignbare modulo s(ellers tall 1,2,... s-1 ville være sammenlignbar modulo s.
Notater
1) I denne artikkelen vil ordet tall bety et heltall.
Litteratur
- 1. K. Irland, M. Rosen. Klassisk introduksjon til moderne tallteori. - M: Mir, 1987.
- 2. G. Davenport. Høyere aritmetikk. - M: Nauka, 1965.
- 3. P.G. Lejeune Dirichlet. Forelesninger om tallteori. - Moskva, 1936.
Fradragsklasser. Fradragssystemer
Kort informasjon fra teorien
Ved å bruke divisjonsteoremet med en rest, kan settet med heltall deles inn i en rekke klasser. Tenk på et eksempel. La være m = 6. Da har vi seks partisjonsklasser av settet med heltall modulo 6:
![]() r = 1;
r = 1;
![]() r = 2;
r = 2;
![]() r = 3;
r = 3;
![]() r = 4;
r = 4;
![]() r = 5;
r = 5;
hvor gjennom r betegner resten av et helt tall delt på 6.
Husk divisjonsteoremet med en rest:
Teorem: Del et tall med et tall , , med en rest, og finn deretter et par heltall q Og r, slik at følgende betingelser er oppfylt: ![]() .
.
Det er lett å bevise det for alle heltall men og divisjon med en rest er mulig og tall q Og r er entydig definert. I vårt eksempel er det komplette systemet med minst ikke-negative rester settet (0, 1, 2, 3, 4, 5); det komplette systemet med minst positive rester er settet (0, 1, 2, 3, 4, 5); et komplett system med de minst absolutte restene - et sett (-2, -1, 0, 1, 2, 3); det reduserte systemet av rester er settet (1,5), siden ; faktor-sett
En metode for å utføre aritmetiske operasjoner på gitte heltall er basert på enkle tallteoriprinsipper. Ideen med denne metoden er at heltall er representert i et av de ikke-posisjonelle systemene - i systemet med gjenværende klasser. Nemlig: i stedet for operasjoner på heltall, opererer de med restene av å dele disse tallene med forhåndsvalgte primtall - moduler ![]() .
.
Oftest tallene ![]() velg fra et sett med primtall.
velg fra et sett med primtall.
La være ![]()
![]() …,
…, ![]() .
.
Siden divisjonsteoremet med resten finner sted i ringen av heltall, dvs. hvor , så ringen Z, per definisjon, er euklidisk.
Dermed kan du som tall velge resten fra å dele tallet MEN på p i hhv.
Restsystemet lar deg utføre aritmetiske operasjoner på et begrenset sett med tall uten å gå utover det. Komplett system med fradrag modulo n er et hvilket som helst sett med n parvis uforlignelig modulo n hele tall. Vanligvis som et komplett system av rester modulo n ta de minste ikke-negative restene
Deling av heltall en Og m det viser seg kvotient q og resten r , slik at
a = m q + r, 0 r m-1. Rest r kalt FRADRAG ohm modulo m.
For eksempel for m = 3 og for m =5 vi får:
| a = m q + r, m = 3 | a = m q + r, m = 5 |
| 0 = 3 + 0 | 0 = 5 + 0 |
| 1 = 3 + 1 | 1 = 5 + 1 |
| 2 = 3 + 2 | 2 = 5 + 2 |
| 3 = 3 + 0 | 3 = 5 + 3 |
| 4 = 3 + 1 | 4 = 5 + 4 |
| 5 = 3 + 2 | 5 = 5 + 0 |
| 6 = 3 + 0 | 6 = 5 + 1 |
| 7 = 3 + 1 | 7 = 5 + 2 |
Hvis resten er null ( r=0 ), så sier de det m deler en hele (eller m flere en ), som betyr m en , og tallene q Og m kalles divisorer en . Åpenbart 1 en Og en en . Hvis en har ingen andre divisorer enn 1 Og men , deretter men er et primtall, ellers men kalt et sammensatt nummer. Største positive deler d to tall en Og m kalt den største felles divisor (GCD) og betegner d = (a, m). Hvis GCD (a,m)=1 , deretter en Og m har ingen felles divisorer annet enn 1 , og sies å være coprime med hensyn til hverandre.
Til hver FRADRAG på r = 0, 1, 2,..., m-1 tilsvarer et sett med heltall a, b,... De sier at tall med det samme FRADRAG er modulo-sammenlignbare og er betegnet med a b(mod m) eller (a b) m .
For eksempel når m = 3 :
For eksempel når m = 5 :
Tall men , som er sammenlignbare modulo m , danner en klasse av dem FRADRAG r og er definert som a = m q + r.
Tall men også kalt FRADRAG modulo m . Ikke-negativ FRADRAG a = r (på q=0 ) tar verdier fra intervallet , danner et komplett system av minste rester modulo m.
FRADRAG men
, tar verdier fra intervallet [-( ,…,( ]
, kl merkelig m
eller fra intervallet [-
![]() på til og med m
danne et komplett system av absolutt minste FRADRAG s modulo m.
på til og med m
danne et komplett system av absolutt minste FRADRAG s modulo m.
For eksempel når m = 5 klasser med minst rester dannes
r = 0, 1, 2, 3, 4, a = -2, -1, 0, 1, 2. Begge gitte tallsett danner komplette systemer fradrag s modulo 5 .
Klasse FRADRAG, hvis elementer er coprime med modulen m
kalles redusert. Euler-funksjonen bestemmer hvor mye FRADRAG fra det komplette systemet med minste rester modulo m coprime med m . Når inaktiv m=p vi har = p-1.
Definisjon. Det maksimale settet med parvis uforlignelige modulo m tall primer med m , er kalt redusert fradragssystem modulo m. Ethvert redusert system av rester modulo m inneholder elementer, hvor er Euler-funksjonen.
Definisjon. Et hvilket som helst tall fra ekvivalensklassen єm vi ringer fradrag ohm modulo m. Samlet fradrag s, tatt en fra hver ekvivalensklasse єm, kalles det komplette systemet fradrag s modulo m(i fullt system fradrag ov, altså totalt m biter av tall). Direkte restene selv når dividert med m kalles de minst ikke-negative fradrag ami og, selvfølgelig, danner et komplett system fradrag s modulo m. Fradrag r kalles absolutt minste hvis ïrï er den minste blant modulene fradrag s av denne klassen.
Eksempel. Sjekk om tallene 13, 8, - 3, 10, 35, 60 danner et komplett system av rester modulo m=6.
Løsning: Per definisjon danner tall et komplett system av rester modulo m, hvis det er nøyaktig m av dem og de er parvis uforlignelige modulo m.
Parvis uforlignbarhet kan testes ved å erstatte hvert tall med den minste ikke-negative resten; hvis det ikke er gjentakelser, så er det et komplett system med fradrag.
La oss bruke divisjonsteoremet med en rest: a = m q + r.
13 = 6 2 + 1 13 1 (mod 6); 8 = 6 1 + 2 8 2 (mod 6);
3 = 6 (-1) + 3 -3 3 (mod 6); 10 = 6 1 + 4 10 4 (mod 6);
35 = 6 5 + 5 35 5 (mod 6); 60 = 6 10 + 0 60 0 (mod 6).
Vi fikk en rekke tall: 1, 2, 3, 4, 5, 0, det er nøyaktig 6 av dem, det er ingen repetisjoner og de er parvis uforlignelige. Det vil si at de danner et komplett system av rester modulo m = 6.
Eksempel. Erstatt med den minste absolutte verdien, samt den minste positive resten 185 modulo 16.
Løsning. La oss bruke divisjonsteoremet med en rest:
185 = 16 11 + 9 185 9 (mod 16).
Eksempel. Sjekk om det dannes tall (13, -13, 29, -9) det reduserte systemet av rester modulo m=10.
Løsning: Ethvert redusert system av rester modulo m inneholder elementer, hvor er Euler-funksjonen. I vårt tilfelle =4, fordi blant de naturlige tallene er bare 1, 3, 7, 9 relativt prime til 10 og ikke overskrider det. Det vil si at det er mulig at disse fire tallene utgjør det ønskede systemet. La oss sjekke disse tallene for deres parvise uforlignbarhet: =4, fordi blant naturlige tall er bare 1, 3, 7, 9 relativt prime til 10 og overskrider det ikke. Det vil si at det er mulig at disse fire tallene utgjør det ønskede systemet. La oss sjekke disse tallene for deres parvise uforlignbarhet: m .
Valg 1. en= 185, m = 12; Alternativ 2. a = 84, m = 9;
Alternativ 3. en= 180, m = 10; Alternativ 4. a = 82, m = 9;
Alternativ 5. en= 85, m = 11; Alternativ 6. a = 84, m = 8;
Alternativ 7. en= 103, m = 87; Alternativ 8. a = 84, m = 16;
Alternativ 9. en= 15, m = 10; Alternativ 10. a = 81, m = 9;
Alternativ 11. en= 85, m = 15; Alternativ 12. a = 74, m = 13;
Alternativ 13. en= 185, m = 16; Alternativ 14. a = 14, m = 9;
Alternativ 15. en= 100, m = 11; Alternativ 16. a = 484, m = 15;
Alternativ 17. en= 153, m = 61; Alternativ 18. a = 217, m = 19;
Alternativ 19. en= 625, m = 25; Alternativ 20. a = 624, m = 25;
Oppgave 3. Skriv ned det komplette og reduserte systemet av minst
Punkt 17. Komplette og reduserte fradragsordninger.
I forrige avsnitt ble det bemerket at forholdet єm sammenlignbarhet modulo m er en ekvivalensrelasjon på settet med heltall. Denne ekvivalensrelasjonen induserer en partisjon av settet med heltall i klasser av ekvivalente elementer, dvs. tall er kombinert i én klasse, og gir når de deles på m de samme restene. Antall ekvivalensklasser єm(Eksperter vil si - "ekvivalensindeks єm") er nøyaktig lik m .
Definisjon. Et hvilket som helst tall fra ekvivalensklassen єm vil bli kalt resten modulo m. Sett med rester tatt en fra hver ekvivalensklasse єm, kalles det komplette systemet av rester modulo m(i hele fradragssystemet, derfor totalen m biter av tall). Direkte restene selv når dividert med m kalles de minst ikke-negative restene og danner selvfølgelig et komplett system av rester modulo m. En rest r sies å være absolutt minst hvis rp er den minste blant restmodulene i den gitte klassen.
Eksempel: La være m= 5. Deretter:
0, 1, 2, 3, 4 - de minste ikke-negative restene;
2, -1, 0, 1, 2 er absolutt de minste restene.
Begge reduserte sett med tall danner komplette systemer av rester modulo 5 .
Lemma 1. 1) Eventuelle m stykker i par ikke sammenlignbare i modul m tall danner et komplett system av rester modulo m .
2) Hvis men Og m coprime, og xm, deretter verdiene til den lineære formen øks+b, hvor b- et hvilket som helst heltall, kjøres også gjennom hele systemet av rester modulo m .
Bevis. Påstand 1) er åpenbar. La oss bevise påstand 2). Tall øks+b glatt m tingene. La oss vise at de ikke er sammenlignbare med hverandre modulo m. Vel la for noen annerledes x 1 Og x2 fra hele fradragssystemet viste det seg at akse 1 +b є akse 2 +b(mod m). Så, ved egenskapene til sammenligninger fra forrige avsnitt, får vi:
akse 1 - akse 2 (mod m)
x 1 x 2 (mod m)
- en motsetning til hva x 1 Og x2 er forskjellige og hentet fra hele fradragssystemet.
Siden alle tall fra en gitt ekvivalensklasse є er hentet fra ett tall i en gitt klasse ved å legge til et tall som er et multiplum av m, så har alle tall fra denne klassen modulo m samme største felles deler. Av noen grunner, de fradragene som har med modulen m den største felles divisor lik én, dvs. rester som er relativt prime i forhold til modulen.
Definisjon. Det reduserte systemet av rester modulo m er settet av alle rester fra hele systemet coprime med modulen m .
Det reduserte systemet velges vanligvis fra de minste ikke-negative restene. Det er klart at det reduserte systemet av rester modulo m inneholder j ( m) biter av rester, hvor j ( m) er Euler-funksjonen, antall tall mindre enn m og coprime med m. Hvis du allerede har glemt Euler-funksjonen på dette tidspunktet, se på avsnitt 14 og forsikre deg om at det ble sagt noe om det der.
Eksempel. La være m= 42. Da er det reduserte systemet av rester:
1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.
Lemma 2. 1) Enhver j ( m) tall som er parvis uforlignelige modulo m og relativt prime til modulen, danner et redusert system av rester modulo m .
2) Hvis (a, m) = 1 Og x går gjennom det reduserte systemet av rester modulo m, deretter øks går også gjennom det reduserte systemet av rester modulo m .
Bevis. Påstand 1) er åpenbar. La oss bevise påstand 2). Tall øks er parvis uforlignelige (dette er bevist på samme måte som i Lemma 1 i dette underavsnittet), er det nøyaktig j ( m) tingene. Det er også klart at de alle er relativt prime til modulen, fordi (a,m)=1, (x,m)=1 X (ax.m)=1. Altså tallene øks danne det reduserte fradragssystemet.
Dette er definisjonene og grunnleggende egenskapene til de fulle og reduserte systemene av rester, men i bagasjen av matematisk kunnskap er det fortsatt en rekke svært interessante og nyttige fakta om systemene av rester. Hvis vi tier om dem i denne paragrafen, vil dette, er jeg redd, være et direkte brudd på den russiske føderasjonens lov om informasjon, hvis ondsinnede fortielse, i henhold til denne loven, er en administrativ og til og med strafferettslig straff. handling. I tillegg, uten kjennskap til ytterligere viktige egenskaper ved fradragssystemer, vil paragraf 17 vise seg å være svært kort. La oss fortsette.
Lemma 3. La være m 1, m 2, ..., m k er parvise coprime og m 1 m 2 ...m k =M 1 m 1 =M 2 m 2 =...=M k m k, hvor
1) Hvis x 1, x 2, ..., x k kjøre gjennom komplette systemer av rester modulo m 1, m 2, ..., m k kjøre gjennom hele systemet av rester modulo m=m 1 m 2 ...m k .
2) Hvis x 1, x 2, ..., x k kjøre gjennom de reduserte systemene av rester modulo m 1, m 2, ..., m k henholdsvis, deretter verdiene til den lineære formen løpe gjennom det reduserte systemet av rester modulo m=m 1 m 2 ...m k .
Bevis.
1) Form M 1 x 1 +M 2 x 2 + ...+M k x k tar tydeligvis m 1 m 2 ...m k =m verdier. La oss vise at disse verdiene er parvis uforlignelige. Vel la
M 1 x 1 +M 2 x 2 + ...+M k x k є M 1 x 1 C +M 2 x 2 C + ...+M k x k C (mod m)
Hva som helst Mj, annerledes enn Ms, flere m s. Fjerne venstre og høyre ledd i den siste sammenligningen, multipler av m s, vi får:
M s x s є M s x s C (mod m s) Yu x s є x s C (mod m s)
- en motsetning til hva x s går gjennom hele systemet av rester modulo m s .
2). Formen M 1 x 1 +M 2 x 2 + ...+M k x k tar tydeligvis j ( m 1) j ( m2) Ch ... Ch j ( m k) = j ( m 1 m 2 W ... W m k)= j ( m) (Euler-funksjonen er multiplikativ!) av forskjellige verdier, som modulo m=m 1 m 2 ...m k parvis uforlignelig. Det siste er lett bevist med argumenter som ligner de som ble brukt i beviset for påstand 1) i dette lemmaet. Fordi ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=(M s x s ,m s)=1 for hver 1 J s J k, deretter ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=1, derav settet med verdier til skjemaet M 1 x 1 +M 2 x 2 + ...+M k x k danner et redusert system av rester modulo m .
Lemma 4. La være x 1, x 2, ..., xk, x kjøre for fullt, og x 1, x 2,..., x k, x– kjøre gjennom de reduserte systemene av rester i moduler m 1, m 2, ..., m k Og m=m 1 m 2 ...m k henholdsvis hvor (m i m j)=1 på jeg № j. Deretter brøker matche med brøker (x/m), og brøker matche med brøker (x/m) .
Bevis. Beviset for begge påstandene til Lemma 4 er enkelt å få ved å bruke den forrige Lemma 3 etter at du har gitt hver sum (x 1 /m 1 + x 2 /m 2 +...+x k /m k ) Og ( x 1 /m 1 + x 2 /m 2 +...+ x k /m k ) til en fellesnevner:
(x 1/m 1 +x 2/m 2 +...+x k/m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ;
( x 1 /m 1 + x 2 /m 2 +...+ x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ,
hvor Mj =m1 ...m j-1 m j+1 ...m k .
Hvis vi nå tar i betraktning at brøkdelene av tallene oppnådd ved å dele med modulo m alle to tall som er sammenlignbare i modul m, er like (de er like r/m, hvor r er den minste ikke-negative resten fra den gitte klassen), da blir påstandene til det nåværende lemma åpenbare.
I resten av denne delen vil det mest interessante skje - vi vil summere de komplekse røttene m potens av 1, og avslører fantastiske sammenhenger mellom rotsummer, restsystemer og den allerede kjente multiplikative Möbius-funksjonen m ( m) .
Betegn med e k k-te rot m- oh grad fra enhet:
Vi husker disse formene for å skrive komplekse tall godt fra det første året. Her k=0,1,...,m-1– går gjennom hele systemet av rester modulo m .
Husk at beløpet e 0 + e 1 +...+ e m-1 alle røtter m enhetskraften er null for noen m. Faktisk, la e 0 + e 1 +...+ e m-1 =a. La oss multiplisere denne summen med et tall som ikke er null e 1 . En slik multiplikasjon geometrisk i det komplekse planet betyr rotasjonen av det korrekte m-gon, ved toppene der røttene er plassert e 0 , e 1 ,..., e m-1, til en vinkel som ikke er null 2p/m. Det er klart at i dette tilfellet roten e 0 gå til root e 1, rot e 1 gå til root e 2, etc., og roten e m-1 gå til root e 0, dvs. sum e 0 + e 1 +...+ e m-1 Vil ikke endre seg. Vi har e1a=a, hvor a=0 .
Teorem 1. La være m>0- et heltall, en O Z , x går gjennom hele systemet av rester modulo m. Så hvis men flere m, deretter

ellers når men ikke et multiplum m ,
 .
.
Bevis. På men flere m vi har: a=md Og
På men ikke delelig med m, del telleren og nevneren til brøken er på d er den største felles deleren men Og m, får vi en irreduserbar brøk a 1 /m 1. Så, ved Lemma 1, en 1 x vil kjøre gjennom hele systemet av rester modulo m. Vi har:
fordi summen av alle røttene til graden m 1 fra enhet er lik null.
Husk at roten e k m enhetskraften kalles antiderivativ hvis dens indeks k gjensidig enkelt med m. I dette tilfellet, som bevist i det første året, påfølgende grader e k 1, e k 2 ,..., e k m-1 rot e k danner hele settet med røtter m kraften fra enhet eller med andre ord, e k er en generator av den sykliske gruppen av alle røtter m grad fra enhet.
Åpenbart antall forskjellige primitive røtter m enhetskraften er lik j ( m), hvor j er Euler-funksjonen, siden indeksene til primitive røtter danner et redusert system av rester modulo m .
Teorem 2. La være m>0 er et heltall, x går gjennom det reduserte systemet av rester modulo m. Deretter (summen av de primitive røttene til graden m):

hvor m ( m) er Möbius-funksjonen.
Bevis. La være m=p 1 a 1 p 2 a 2 ... p k a k er den kanoniske utvidelsen av tallet m ; m 1 \u003d p 1 a 1 , m 2 \u003d p 2 a 2 , m 3 \u003d p 3 a 3; x i går gjennom det reduserte systemet av rester modulo m jeg. Vi har:

På a s = 1 det viser seg at bare roten e 0 = 1 er ikke primitiv, så summen av alle primitive røtter er summen av alle røtter minus én:

så hvis m fri for firkanter (dvs. ikke delelig med r2, kl r>1), deretter

Hvis noen indikator som større enn én (dvs. m delt på r2, kl r>1), deretter summen av alle primitive røtter til graden m s er summen av alle røttene til graden m s minus summen av alle ikke-primitive røtter, dvs. alle røtter av en eller annen grad mindre m s. Nøyaktig hvis m s =p s m s *, deretter:

Nå, kjære lesere, når jeg har presentert for deres vurdering en ganske betydelig mengde informasjon om de fullstendige og reduserte fradragssystemene, kan ingen anklage meg for ondsinnet brudd på den russiske føderasjonens lov om informasjon ved å holde tilbake den, så jeg avslutter dette avsnitt med tilfredshet.
| gåter |
1 . Skriv ned på et papir alle de minste ikke-negative restene og alle de absolutt minste restene a) modulo 6, b) modulo 8. Rett nedenfor, skriv ned de gitte fradragssystemene for disse modulene. Tegn separat på det komplekse planet røttene til den sjette og åttende enhetsrøttene, i begge figurene sirkler de primitive røttene og finn summen i hvert tilfelle. 2 . La være e- primitiv rot 2n fra en enhet. Finn beløpet: 1+ e + e 2 +...+ e n-1 . 3 . Finn summen av alle primitive røtter: a) 15.; b) 24.; c) 30. grad fra enhet. 4 . Finn summen av alle mulige produkter av primitive røtter n grad fra én, tatt av to. 5 . finne summen k-x potenser av alle røtter n grad fra enhet. 6 . La være m>1 , (a, m)=1 , b er et heltall, X går gjennom hele og x går gjennom det reduserte systemet av rester modulo m. Bevis det: men) b) 7 . Bevis det:
hvor R går gjennom alle primdelere av et tall men . |
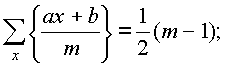

 ,
,